Diagrama de Venn
Los diagramas de Venn son esquemas usados en la teoría de conjuntos, tema de interés en matemáticas, lógica de clases y razonamiento diagramático. Estos diagramas muestran colecciones (conjuntos) de cosas (elementos) por medio de líneas cerradas. La línea cerrada exterior abarca a todos los elementos bajo consideración, el conjunto universal U.
Los diagramas de Venn fueron ideados hacia 1880 por John Venn.
Ejemplos:
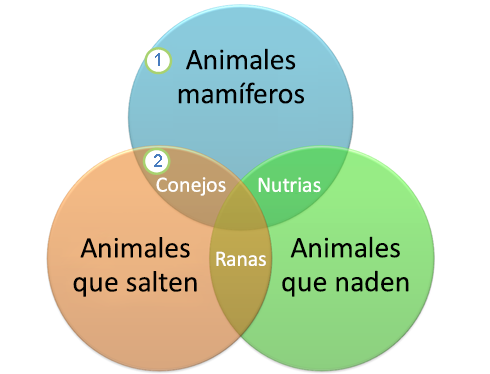


(Coloque esa ya que tal vez así sea más sencillo de entender, tomando en cuenta a la sociedad de hoy en día xdxd)
Operaciones de conjuntos
Unión de conjuntos
Sean {\displaystyle A}
 y {\displaystyle B}
y {\displaystyle B} dos conjuntos. Se define la unión de {\displaystyle A}
dos conjuntos. Se define la unión de {\displaystyle A} con {\displaystyle B}
con {\displaystyle B} , denotada por {\displaystyle A\cup B}
, denotada por {\displaystyle A\cup B} (que se lee A unión B), por el conjunto{\displaystyle A\cup B=\{x:x\in A\vee x\in B\}}
(que se lee A unión B), por el conjunto{\displaystyle A\cup B=\{x:x\in A\vee x\in B\}}
En un Diagrama de Venn, la unión de dos conjuntos {\displaystyle A}
 y {\displaystyle B}
y {\displaystyle B} , dependiendo de cómo se relacionan entre ellos, se ve como sigue:
, dependiendo de cómo se relacionan entre ellos, se ve como sigue:
Unión de conjuntos
En términos prácticos, la unión de dos conjuntos es el conjunto formado por los elementos de cualquiera de los dos conjuntos.
Ejemplo
Si tenemos los conjuntos {\displaystyle A=\{1,2,3,4,5\}} y {\displaystyle B=\{3,4,5,6,7,8\}}
y {\displaystyle B=\{3,4,5,6,7,8\}} , la unión de ellos es el conjunto{\displaystyle A\cup B=\{1,2,3,4,5,6,7,8\}}
, la unión de ellos es el conjunto{\displaystyle A\cup B=\{1,2,3,4,5,6,7,8\}}
Propiedad de la unión de conjunto
La unión de conjunto cumple la siguiente propiedad.
{\displaystyle A\cup A=A}
{\displaystyle A\cup B=B\cup A}
{\displaystyle A\cup (B\cup C)=(A\cup B)\cup C}
{\displaystyle A\cup \phi =A}
Si {\displaystyle A\subseteq B\Rightarrow A\cup B=B}
Intersección de Conjuntos
Sean {\displaystyle A} y {\displaystyle B}
y {\displaystyle B} dos conjuntos. Se define la intersección de {\displaystyle A}
dos conjuntos. Se define la intersección de {\displaystyle A} y {\displaystyle B}
y {\displaystyle B} , denotada por {\displaystyle A\cap B}
, denotada por {\displaystyle A\cap B} (que se lee A intersección B), por el conjunto{\displaystyle A\cap B=\{x:x\in A\wedge x\in B\}}
(que se lee A intersección B), por el conjunto{\displaystyle A\cap B=\{x:x\in A\wedge x\in B\}}
En un Diagrama de Venn, la intersección de dos conjuntos {\displaystyle A} y {\displaystyle B}
y {\displaystyle B} , dependiendo de cómo se relacionan entre ellos, se ve como sigue:
, dependiendo de cómo se relacionan entre ellos, se ve como sigue:

En términos prácticos, la unión de dos conjuntos es el conjunto formado por los elementos de cualquiera de los dos conjuntos.
Ejemplo
Si tenemos los conjuntos {\displaystyle A=\{1,2,3,4,5\}}
 y {\displaystyle B=\{3,4,5,6,7,8\}}
y {\displaystyle B=\{3,4,5,6,7,8\}} , la unión de ellos es el conjunto{\displaystyle A\cup B=\{1,2,3,4,5,6,7,8\}}
, la unión de ellos es el conjunto{\displaystyle A\cup B=\{1,2,3,4,5,6,7,8\}}
Propiedad de la unión de conjunto
La unión de conjunto cumple la siguiente propiedad.
{\displaystyle A\cup A=A}

{\displaystyle A\cup B=B\cup A}

{\displaystyle A\cup (B\cup C)=(A\cup B)\cup C}

{\displaystyle A\cup \phi =A}

Si {\displaystyle A\subseteq B\Rightarrow A\cup B=B}

Intersección de Conjuntos
Sean {\displaystyle A}
 y {\displaystyle B}
y {\displaystyle B} dos conjuntos. Se define la intersección de {\displaystyle A}
dos conjuntos. Se define la intersección de {\displaystyle A} y {\displaystyle B}
y {\displaystyle B} , denotada por {\displaystyle A\cap B}
, denotada por {\displaystyle A\cap B} (que se lee A intersección B), por el conjunto{\displaystyle A\cap B=\{x:x\in A\wedge x\in B\}}
(que se lee A intersección B), por el conjunto{\displaystyle A\cap B=\{x:x\in A\wedge x\in B\}}
En un Diagrama de Venn, la intersección de dos conjuntos {\displaystyle A}
 y {\displaystyle B}
y {\displaystyle B} , dependiendo de cómo se relacionan entre ellos, se ve como sigue:
, dependiendo de cómo se relacionan entre ellos, se ve como sigue:
Intersección de Conjuntos
En términos prácticos, la intersección de dos conjuntos es el conjunto formado por los elementos comunes a ambos conjuntos.
Si tenemos los conjuntos {\displaystyle A=\{1,2,3,4,5,6,7,8\}}
 y {\displaystyle B=\{4,5,6,7\}}
y {\displaystyle B=\{4,5,6,7\}} , el conjunto intersección es{\displaystyle A\cap B=\{4,5,6,7\}}
, el conjunto intersección es{\displaystyle A\cap B=\{4,5,6,7\}}
Nota: Dos pares de conjuntos {\displaystyle A}
 y {\displaystyle B}
y {\displaystyle B} se llaman disjuntos siempre que {\displaystyle A\cap B=\phi }
se llaman disjuntos siempre que {\displaystyle A\cap B=\phi } .
.Propiedades de la intersección de conjuntos
La intersección de conjuntos cumple con las siguientes propiedades
{\displaystyle A\cap A=A}

{\displaystyle A\cap B=B\cap A}

{\displaystyle A\cap (B\cap C)=(A\cap B)\cap C}

{\displaystyle A\cap \phi =\phi }

Si {\displaystyle A\subseteq B\Rightarrow A\cap U=A}

Simbologia

Distribución de un conjunto


Otra representacion:
 Dado que los diagramas de Venn puede representar conjuntos con cualquier forma se puede hacer un sinfín de representaciones. Sin embargo estas (la mayoría ) tienden a confundir.
Dado que los diagramas de Venn puede representar conjuntos con cualquier forma se puede hacer un sinfín de representaciones. Sin embargo estas (la mayoría ) tienden a confundir.Ejercicios
Problema 1
A la entrada de la escuela, se les aplicó a 156 niños una encuesta respecto a sus juguetes favoritos.
La encuesta arrojó los siguientes resultados:
▪ A 52 niños les gustaba el balón; a 63 les gustaban los carritos; a 87 les gustaban los videojuegos.
▪ Además algunos de ellos coinciden en que les gustaba mas de un juguete: 26 juegan con el balón y carritos; 37 juegan con carritos y videojuegos; 23 juegan con el balón y los videojuegos; por ultimo 7 expresaron su gusto por los tres.
a) ¿A cuántos niños les gusta otro juguete no mencionado en la encuesta?
b) ¿A cuántos niños les gusta solamente jugar con los videojuegos?
c) ¿A cuántos niños les gusta solamente jugar con el balón?
Problema 2
La secretaría de educación municipal requiere la provisión de 29 cargos docentes en las siguientes áreas: 13 profesores en matemáticas, 13 profesores en física y 15 en sistemas. Para el cubrimiento de los cargos se requiere que: 6 dicten matemáticas y física, 4 dicten física y sistemas y 5 profesores dicten matemáticas y sistemas.
Determinar:
a) ¿Cuántos profesores se requiere que dicten las 3 áreas?
b) ¿Cuántos profesores se requiere para dictar matemáticas únicamente?
c) ¿Cuántos profesores se requiere para dictar matemáticas y sistemas pero no física?
Fuentes:
https://es.wikibooks.org/wiki/%C3%81lgebra_Fundamental/Operaciones_entre_Conjuntos
https://umsistemas.wordpress.com/2016/12/15/2-diagramas-de-euler-venn-capitulo-1/
http://profe-alexz.blogspot.com/2014/01/diagramas-de-venn-con-3-conjuntos.html
Comentarios
Publicar un comentario